数学理论
绿色代表欧氏距离(直线距离)。
红线代表曼哈顿距离,蓝色和黄色是等价的曼哈顿距离。
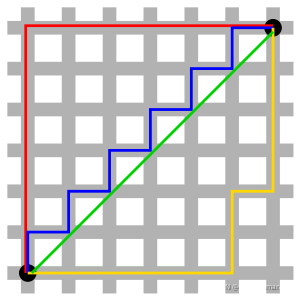
曼哈顿距离在2维平面是两点在纵轴上的距离加上在横轴上的距离,即:
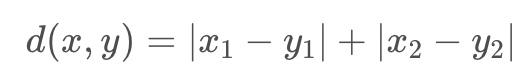
- 曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同。
n维空间中的欧式(欧几里得,Euclidean Distance)距离:
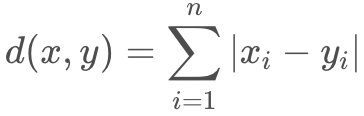
曼哈顿距离的Python实现
1
2
3
4
5
def ManhattanDistance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.sum(np.abs(x-y))
曼哈顿距离在推荐系统中的实践
下面案例中分别使用了基于用户和项目的两种推荐系统
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
class Recommendation:
def __init__(self):
# 将上面数据作为此处初始化数据
self.information = data
'''
data格式:
{用户:{游戏(或其他项目)} }
如:
{'Tom': {'A': 6.0, 'B': 7.0, 'C': 9.0,'D': 2.0, 'E': 4.0, 'F': 10.0},
'Jerry': {'A': 3.0, 'B': 7.0, 'C': 2.0,'D': 5.0, 'E': 6.0, 'F': 9.0},
'Hank': {'A': 5.0, 'B': 7.0,'D': 2.0, 'E': 8.0, 'F': 5.0},
'Alex': {'B': 6.0, 'C': 8.0,'D': 5.0, 'E': 6.0,'F': 9.0},
'Cary': {'A': 6, 'B': 8, 'C': 4,'D': 6,'E': 4,'F': 6,},
'Jack': {'A': 2.0, 'B': 7.0,'C': 4,'D': 5.0,'E': 6.0, 'F': 9.0},
'Ben': {'A': 2.0,'D': 6.0,'E': 6.0}}
'''
#计算用户1与用户2的曼哈顿距离
def _cal_mh_dis(self, user1, user2):
# 对原数据进行格式转换操作
goods = self._transform()
distance = 0 # 初始化两用户对某游戏评价的差值
# 循环遍历各游戏
for good in goods:
# 用户1对当前游戏的评分(玩的时长)
user1_good_score = self.information[user1].get(good, 0)
# 用户2对当前游戏的评分
user2_good_score = self.information[user2].get(good, 0)
# 两用户评分差值
score_diff = user1_good_score - user2_good_score
# 如果评分都为0,则差值为0
if user1_good_score == 0 or user2_good_score == 0:
score_diff = 0
# 差值加上 两用户对本游戏评分的差值的绝对值
distance += abs(score_diff)
#返回两个用户对相同物品的评价差值总和
return distance
# 计算用户1和用户2之间的相似度
def _similarity(self, user1, user2):
# 调用上面函数求出曼哈顿距离distance
distance = self._cal_mh_dis(user1, user2)
# 归一化处理,temp越大,两个用户之间的相似度越低
temp = 1 / (distance + 1)
return temp
def _transform(self):
"""
将矩阵用户——物品的键和值进行调换为物品——用户
return:键值调换后的dict: {key=good, value={key=user, value=score}}
如下所示:
{'A': {'Tom': 6.0, 'Jerry': 3.0, 'Hank': 5.0, 'Cary': 6, 'Jack': 2.0, 'Ben': 2.0},
'B': {'Tom': 7.0, 'Jerry': 7.0, 'Hank': 7.0, 'Alex': 6.0, 'Cary': 8, 'Jack': 7.0},}
"""
result = {}
# 遍历用户-游戏dict
for user in self.information:
# 从用户-游戏dict中提取游戏id
for item in self.information[user]:
'''
新的dict为游戏-用户格式
'''
result.setdefault(item, {})
# result[游戏][用户] = 原数据[用户][游戏]的值(打分)
result[item][user] = self.information[user][item]
return result
# 寻找与当前传入user相似度最高的3个用户
def _top_matches(self, user, k=2):
# 各用户相似度键值对
distances = {}
# 取出各用户id赋值为p
for p in self.information.keys():
# 判断是否为当前传入user,若此当前循环到的用户id不是传入的user,则求它们的相似度(p与user)
if p != user:
distances[p] = self._similarity(p, user)
# 排序,找出相似度最高的三位
return sorted(distances.items(), key=lambda x: x[1], reverse=True)[0:k]
# 基于用户的协同过滤算法
def recommend_by_people(self, user):
# 为用户未玩过的游戏打分:基于与用户最相似的其他k个用户对当前物品的评价的加权平均;
# 相似度top_k用户
top_k_users = self._top_matches(user, k=2)
# 转化后的游戏列表
goods = self._transform()
#推荐的游戏, 及推荐分数
recommend = {}
# 相似度之和
simi_sum = 0
# top_k_users的分数之和
score = 0
# 遍历游戏id
for good in goods:
# 当前游戏如果不在用户玩过的列表,则可以进行推荐
if good not in self.information[user].keys():
# 遍历与输入用户相似度最高的几个用户
for i in range(len(top_k_users)):
# 获取top几用户的id
current_user = top_k_users[i][0]
# 判断,当前游戏是否在打分用户玩过的里面;如果是。。。
if good in self.information[current_user].keys():
# 总评分 = 该用户对该游戏的评分 * 该用户与输入用户的相似度
score += self.information[current_user][good] * top_k_users[i][1]
# 相似度之和
simi_sum += top_k_users[i][1]
# 对当前游戏的推荐分数:总评分/相似度之和
recommend[good] = score / simi_sum
# 返回 相似度top几用户对当前用户没玩过的游戏的评分
return recommend
# 计算游戏相似度字典
def _cal_goods_similarity(self):
goods = self._transform() # 所有转换后的游戏数据
users = self.information.keys() # 用户列表
simi_good = 0 # 游戏相似度
# good_simi_dict: {key=i游戏, value={key=j游戏, value=相似度}}
good_simi_dict = {}
# 循环遍历所有游戏
for i in goods:
inner_dict = {}
for j in goods:
# 判断两个游戏是否相同,同一个游戏无法判断相似度
if i != j:
# 遍历玩过当前游戏的所有用户
for p in users:
# 如果用户玩过i游戏且玩过j游戏
if p in goods[i].keys() and p in goods[j].keys():
# 游戏相似度 = i游戏用户的打分 - j游戏用户的打分 的绝对值之和
simi_good += abs(goods[i][p] - goods[j][p])
# i游戏和j游戏的相似度
simi_good = 1 / (simi_good + 1)
# 临时存储j相似度
inner_dict[j] = simi_good
# 存储i游戏与j游戏相似度
good_simi_dict[i] = inner_dict
return good_simi_dict
#基于游戏(项目)进行推荐,传入一个用户
def recommend_by_item(self, user):
# 游戏相似度字典
good_simi_dict = self._cal_goods_similarity()
# 游戏列表
goods = self._transform().keys()
recommend = {} # 推荐结果
# 遍历游戏列表
for good in goods:
# 初始化相似度和推荐指数
simi = 0
score = 0
# 进行判断,good表示传入用户未玩过的游戏
if good not in self.information[user].keys():
# 遍历与当前游戏相似的游戏的键
for i in good_simi_dict[good].keys():
# 如果相似游戏在该玩家玩过的游戏中
if i in self.information[user].keys():
# 得分 = good与当前玩过游戏的相似度 * 玩家玩这款游戏的时长(打分)
score += good_simi_dict[good][i] * self.information[user].get(i, 0)
# 总相似度
simi += good_simi_dict[good][i]
# 当前游戏与玩家玩过的游戏相似度
simi = score / simi
recommend[good] = simi
# 得到推荐结果
return recommend
if __name__ == "__main__":
system = Recommendation()
# 计算两用户间的距离
# 注:user均为实际数据中自己选择的用户
similarity = system._similarity('user1', 'user2')
print("当前两用户的相似度为:{0}".format(similarity))
# 和某用户相似度最高的k个用户
top_k_matches = system._top_matches('user', k=2)
print("与当前用户相似度最高的是:{0}".format(top_k_matches))
# 基于用户的协同过滤推荐
recommendation = system.recommend_by_people("user")
print("给当前用户推荐是:{0}".format(recommendation))
# 基于物品相似度进行推荐
print("基于项目相似度推荐结果:{0}".format(system.recommend_by_item("user")))