K-Means算法(聚类)
通过把样本分离成n个具有相同方差的类的方式来聚集数据,最小化称为惯量(inertia) 或 簇内平方和(within-cluster sum-of-squares) 的标准(criterion)。
该算法 需要指定簇的数量。
它可以很好地扩展到大量样本(large number of samples),并已经被广泛应用于许多不同领域的应用领域。
k-means算法将一组 N 样本 X 划分成 K 不相交的簇 C, 每个都用该簇中的样本的均值
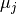
描述。 这个均值(means)通常被称为簇的 “质心(centroids)”; 注意,它们一般不是从 X 中挑选出的点,虽然它们是处在同一个空间。
K-means(K-均值)算法旨在选择一个质心, 能够最小化惯性或簇内平方和的标准:
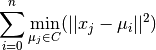
惯性被认为是测量簇内聚程度的度量(measure)。
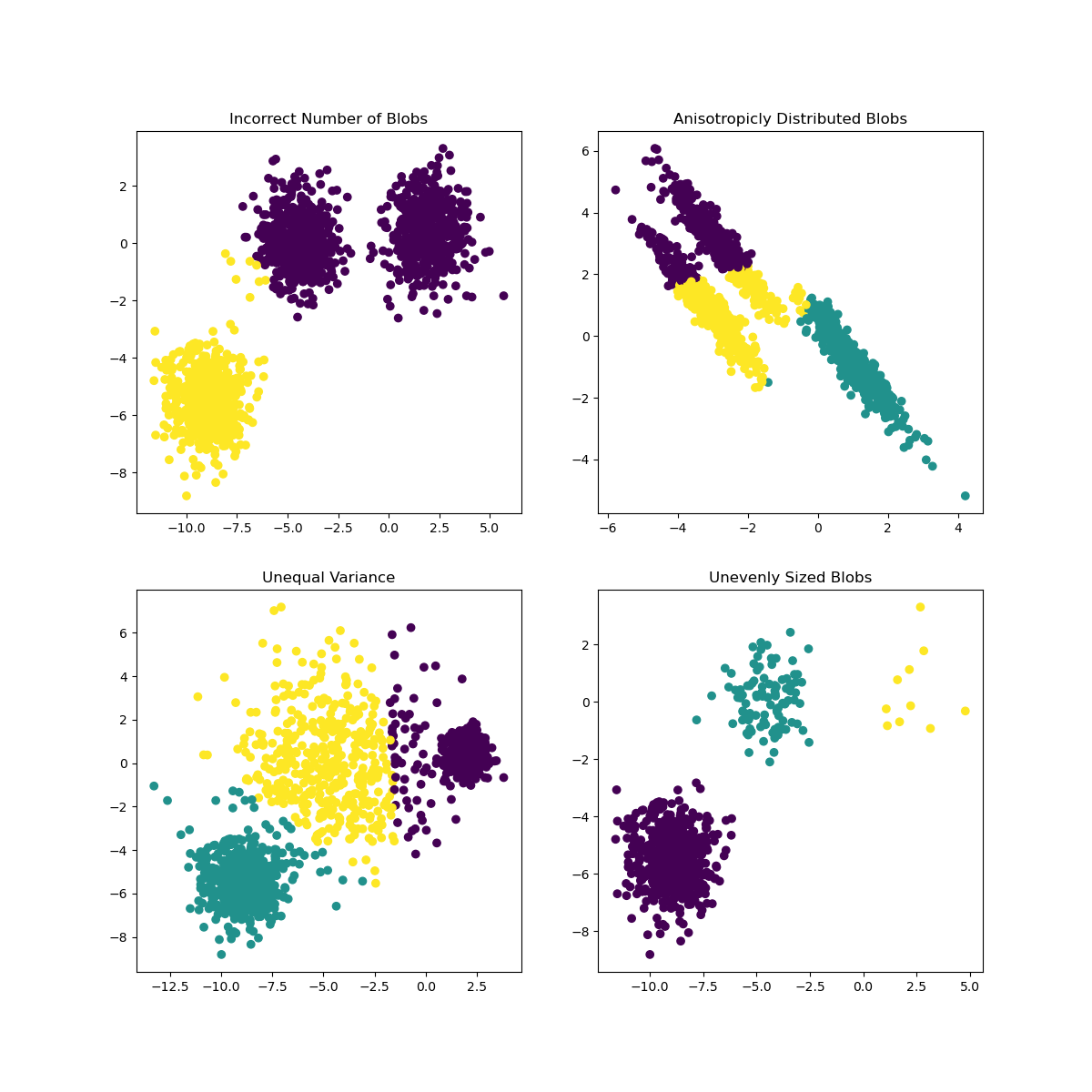
它有各种缺点:
- 惯性假设簇是凸(convex)的和各项同性(isotropic),这并不是总是对的。它对 细长 的簇或具有不规则形状的流行反应不佳。
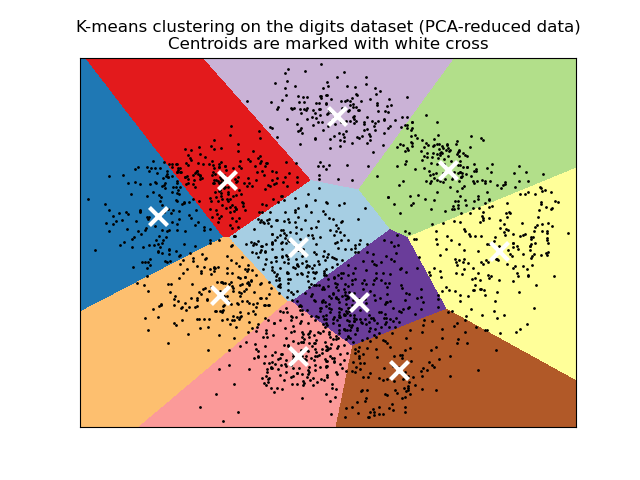
- 惯性不是一个归一化度量(normalized metric): 我们只知道当惯量的值较低是较好的,并且零是最优的。但是在非常高维的空间中,欧氏距离往往会膨胀(这就是所谓的 “维度诅咒/维度惩罚”(curse of dimensionality))。在 k-means 聚类算法之前运行诸如 PCA 之类的降维算法可以减轻这个问题并加快计算速度。
K-means 通常被称为 劳埃德算法(Lloyd’s algorithm) 。简而言之,该算法可分为三个步骤。第一步是选择初始质心,最基本的方法是从 X 数据集中选择 k 个样本。初始化完成后,K-means 由接下来两个步骤之间的循环组成。 第一步将每个样本分配到其最近的质心。第二步通过取分配给每个先前质心的所有样本的平均值来创建新的质心。计算旧的和新的质心之间的差异,并且算法重复这些最后的两个步骤,直到该值小于阈值。换句话说,算法重复这个步骤,直到质心不再显著移动。
K-means 相当于具有小的全对称协方差矩阵(small, all-equal, diagonal covariance matrix)的期望最大化算法(expectation-maximization algorithm)。
该算法也可以通过 Voronoi diagrams(Voronoi图) 的概念来理解。首先,使用当前质心计算点的 Voronoi 图。 Voronoi 图中的每个段(segment)都成为一个单独分离的簇。其次,质心被更新为每个段的平均值。然后,该算法重复此操作,直到满足停止条件。 通常情况下,当迭代之间的目标函数(objective function)的相对减小小于给定的公差值(tolerance value)时,算法停止。在此实现中不是这样: 当质心移动小于公差时,迭代停止。
给定足够的时间,K-means 将总是收敛的,但这可能是局部最小。这很大程度上取决于质心的初始化。 因此,通常会进行几次初始化不同质心的计算。帮助解决这个问题的一种方法是 k-means++ 初始化方案,它已经在 scikit-learn 中实现(使用 init=’k-means++’ 参数)。 这将初始化质心(通常)彼此远离,导致比随机初始化更好的结果,如参考文献所示。
该算法支持样本权重功能,该功能可以通过参数sample_weight实现。该功能允许在计算簇心和惯性值的过程中,给部分样本分配更多的权重。 例如,给某个样本分配一个权重值2,相当于在dataset X 中增加一个该样本的拷贝。
存在一个参数,以允许 K-means 并行运行,称为 n_jobs。给这个参数赋予一个正值指定使用处理器的数量(默认值: 1)。值 -1 使用所有可用的处理器,-2 使用全部可用处理器减一,等等。并行化(Parallelization)通常以内存的代价(cost of memory)加速计算(在这种情况下,需要存储多个质心副本,每个作业(job)使用一个副本)。
警告
K-Means 的并行版本不能在 OS X 上运行, 当内部的 numpy 使用 Accelerate 框架。这是预期的行为: Accelerate 可以在 fork 之后调用,但是您需要使用 Python binary 来执行子进程(posix 并不支持多进程处理 )。
K-means 可用于矢量量化(vector quantization)。这是使用以下类型的训练模型的变换方法实现的 KMeans 。
1
2
3
4
5
6
7
#导入所需包
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
1
2
3
#导入数据集
iris = load_iris()
# iris
1
2
3
4
X = iris['data'][:,-2:]
Y = iris['target']
# 可预览数据
# print('data:\n',X,'\n\ntarget:\n',Y)
1
2
3
4
# 划分数据集
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size = 0.7,random_state=0)
# 预览数据形状
X_train.shape
1
output: (45, 2)
1
2
3
# KMeans将数据划分为三簇
km = KMeans(n_clusters=3)
km.fit(X)
1
2
c_points = km.cluster_centers_ #3簇的簇中心坐标
print(c_points)
1
2
3
output: [[1.462 0.246 ]
[5.59583333 2.0375 ]
[4.26923077 1.34230769]]
1
2
labels = km.labels_
print(labels)
1
2
3
4
5
6
output:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 2 1 1 1 1
1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1
1 1]
1
2
y_pred = km.predict(X)
# print(y_pred)
1
2
# 验证法1
# labels == y_pred
1
2
3
4
# 验证法2
from collections import Counter
print(Counter(labels))
print(Counter(y_pred))
1
2
3
output:
Counter({0: 52, 1: 50, 2: 48})
Counter({0: 52, 1: 50, 2: 48})
绘图
1
2
3
4
5
6
7
8
9
10
11
12
ptl_len = X[:,0]
ptl_wid = X[:,1]
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(12,6))
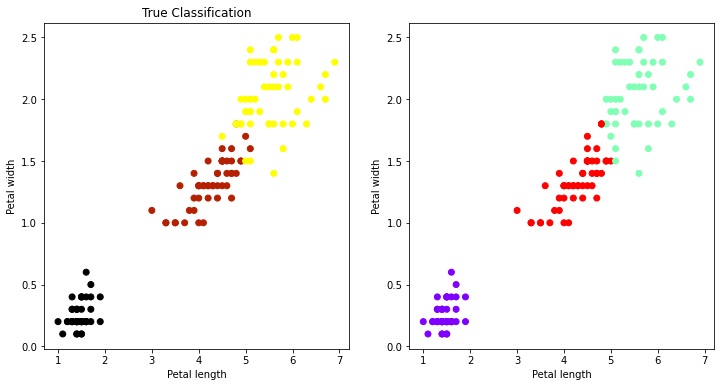
ax1.scatter(ptl_len,ptl_wid,c = Y, cmap=plt.cm.gnuplot)
ax1.set_title('True Classification')
ax1.set_xlabel("Petal length")
ax1.set_ylabel('Petal width')
ax2.scatter(ptl_len,ptl_wid,c = labels, cmap=plt.cm.rainbow)
ax2.set_xlabel("Petal length")
ax2.set_ylabel('Petal width')
plt.show()
代码整合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#导包
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
iris = load_iris() #导入数据
#划分数据集
X = iris['data'][:,-2:]
Y = iris['target']
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size = 0.7,random_state=0)
#kmeans 簇设为3
km = KMeans(n_clusters=3)
km.fit(X)
#3簇的簇中心坐标
c_points = km.cluster_centers_
labels = km.labels_
# 作图
ptl_len = X[:,0]
ptl_wid = X[:,1]
# 自定义图像主题(可参考本文最底部支持样式获取)
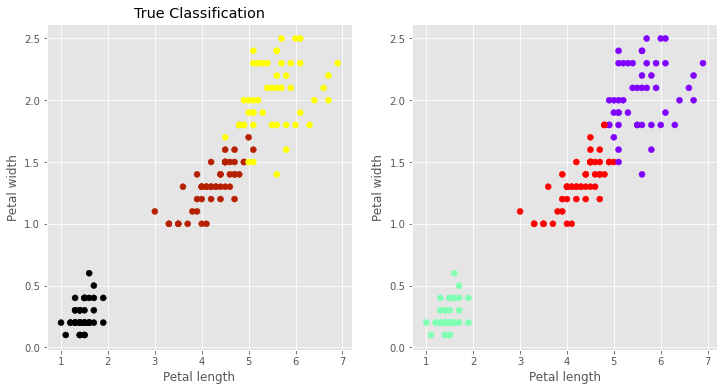
plt.style.use('ggplot')
# 创建画布
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(12,6))
ax1.scatter(ptl_len,ptl_wid,c = Y, cmap=plt.cm.gnuplot)
ax1.set_title('True Classification')
ax1.set_xlabel("Petal length")
ax1.set_ylabel('Petal width')
ax2.scatter(ptl_len,ptl_wid,c = labels, cmap=plt.cm.rainbow)
ax2.set_xlabel("Petal length")
ax2.set_ylabel('Petal width')
plt.show()
Matplotlib.cm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#导包
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
iris = load_iris() #导入数据
#划分数据集
X = iris['data'][:,-2:]
Y = iris['target']
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size = 0.7,random_state=0)
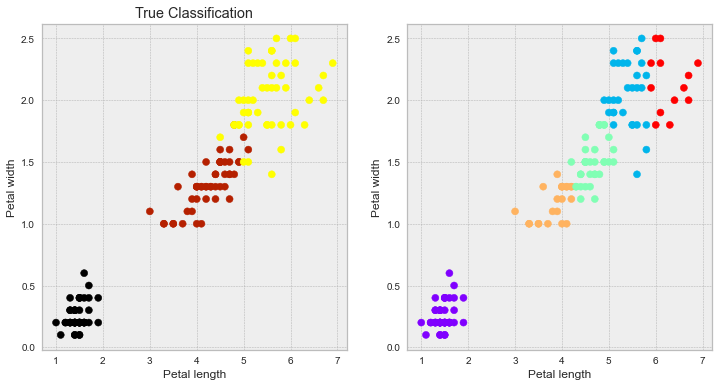
#kmeans 簇设为5
km = KMeans(n_clusters=5)
km.fit(X)
c_points = km.cluster_centers_ #3簇的簇中心坐标
labels = km.labels_
ptl_len = X[:,0]
ptl_wid = X[:,1]
plt.style.use('bmh')
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(12,6))
ax1.scatter(ptl_len,ptl_wid,c = Y, cmap=plt.cm.gnuplot)
ax1.set_title('True Classification')
ax1.set_xlabel("Petal length")
ax1.set_ylabel('Petal width')
ax2.scatter(ptl_len,ptl_wid,c = labels, cmap=plt.cm.rainbow)
ax2.set_xlabel("Petal length")
ax2.set_ylabel('Petal width')
plt.show()
此电脑环境支持的画布样式
1
2
#可用样式查看
print(plt.style.available)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
['Solarize_Light2',
'_classic_test_patch',
'_mpl-gallery',
'_mpl-gallery-nogrid',
'bmh',
'classic',
'dark_background',
'fast',
'fivethirtyeight',
'ggplot',
'grayscale',
'seaborn',
'seaborn-bright',
'seaborn-colorblind',
'seaborn-dark',
'seaborn-dark-palette',
'seaborn-darkgrid',
'seaborn-deep',
'seaborn-muted',
'seaborn-notebook',
'seaborn-paper',
'seaborn-pastel',
'seaborn-poster',
'seaborn-talk',
'seaborn-ticks',
'seaborn-white',
'seaborn-whitegrid',
'tableau-colorblind10']
1